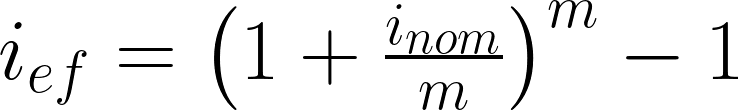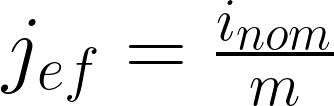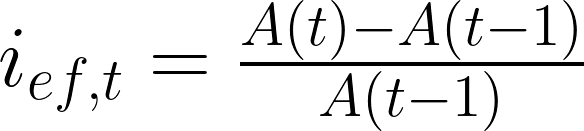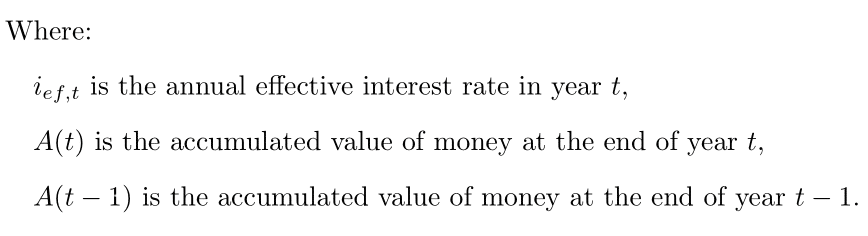Effective Rate of Interest: Definition and Formulas
Actuarial work is strongly associated with money. Calculating reserves, estimating losses, and modeling future profits are some of the examples. Understanding the effective interest rate is crucial to all these problems.
Let’s say you deposit $1,000 into a bank savings account on December 31st, 2024, and a year later, you have a balance of $1,040. This amount is called the accumulated value of money after one year. We can say that your money earned $40 in interest. By dividing the $40 (interest earned) by $1,000 (initial deposit), we get 4%, which is referred to as the annual effective rate of interest for that year.
Alright, now you know everything, and I can end this post (just kidding—there’s still plenty more to learn!).
Picture 1. A $1,000 investment made at the end of 2024 earned $40 in interest during 2025. The annual effective rate of interest for this period is 4%. For simplicity, it is labeled as “annual effective” on the graph.
Below, I will describe the effective rate of interest, starting with its definition and formulas. Then, I will explain how to calculate the annual effective rate of interest based on an annual nominal interest rate.
This is a broad topic, so today, I will focus on introducing the definition of the effective interest rate and a few key formulas. In the next post in the Actuarial Concepts series, I will delve further into this subject.
Let’s buckle up and start exploring this topic!
What is the Effective Rate of Interest?
Simply put, the effective rate of interest (also known as the effective interest rate) is the real interest earned on an investment over a specific period. When we refer to the annual effective rate of interest, we are specifically looking at the interest earned during one year of investment.
Definition
First of all, in this post, when I say real return, I am referring to the return based on the effective rate of interest, without accounting for the inflation rate. The real interest rate, which adjusts the effective interest rate for inflation, will not be discussed in this post. One possible definition of the effective interest rate is as follows:
An effective interest rate is a real return on a savings account or any interest-paying investment when compounding effects are considered.
After reading it, some questions were probably raised about the compounding effects. In the first example I gave in this post, I stated that interest is earned at the end of the year (one year is one compounding period). However, sometimes interest can be earned more frequently, such as semi-annually, quarterly, or monthly. In these cases, there are multiple compounding periods within a single year.
Banks and other institutions often advertise a nominal interest rate for savings accounts rather than the effective rate. While both rates are expressed annually, they are not the same. The nominal rate assumes no compounding within the year, whereas the effective rate accounts for how often interest is earned and reinvested. For example, if interest is compounded monthly, the effective rate will reflect the additional growth generated by reinvesting interest twelve times over the year.
But why do banks tend to provide us with nominal rather than effective interest rates? The answer lies in simplicity and marketing. The nominal rate is easier to communicate and calculate for promotional purposes. It presents a straightforward, appealing figure without requiring explanations of compounding frequency or complex formulas.
Additionally, by not highlighting the effective rate, banks may benefit from customers not fully grasping the differences between accounts with varying compounding periods. This lack of clarity can make nominal rates seem more competitive, even if the effective rate is lower when compounding is less frequent.
Alright, by now, you are aware that nominal and effective interest rates are not the same, and that the effective interest rate represents the real return on investment over a given period of time. But how can we express the effective interest rate as a formula? The next chapter will answer that question.
Formulas
To calculate the annual effective interest rate based on the annual nominal interest rate, we can use the following formula:
Formula 1. Deriving the Annual Effective Interest Rate from the Annual Nominal Interest Rate
Sometimes, a more useful approach is to calculate the effective interest rate for a period shorter than one year, especially when we have an annual nominal interest rate compounded m times per year. In this case, the effective interest rate for one compounding period is equal to:
Formula 2. Effective Interest Rate for One Compounding Period, which Occurs m Times During One Year.
Looking at the first example given at the beginning, we can compute the effective interest rate based on the initial amount of money invested and the amount earned at the end of the investment. The formula for the effective interest rate during this period can be written as:
Formula 3. Annual Effective Interest Rate in Year t.
Each of the presented formulas is useful and helps to fully understand what the effective interest rate represents. First, it can be calculated from the nominal interest rate by dividing it by the number of compounding periods and raising it to the appropriate power. Second, it can be expressed as the real amount of interest earned divided by the initial deposit.
If we look at the interest earned during a single month, it would be referred to as the monthly effective interest rate. Similarly, if we consider the return on investment over two years, we would calculate the 2-year effective interest rate.
Summary
The effective interest rate is essential for fully understanding how the value of money changes over time. It is widely used by actuaries, actuarial analysts, and other professionals working with financial instruments. It describes the real growth of money’s value over a specific period and takes the compounding effect into account.
We can calculate the annual effective interest rate from the annual nominal interest rate or by analyzing the difference in accumulated values of money at the beginning and the end of a year. Additionally, given an annual nominal interest rate compounded m-times in a year, we can calculate the effective interest rate for one compounding period by dividing the nominal rate by m.
As I mentioned at the beginning, this is the first out of two at least posts about effective interest rate. In the next one, I will go with effective interest usage to compute accumulated as well as a present value of an investment. Besides formuals, I will go through a couple of calculational examples.
If you have any questions, or concerns, or are simply interested in this topic, please feel free to leave a comment, send an email, or message me on LinkedIn. I’d be happy to hear your thoughts!
Below, you’ll find some links that further discuss the topics of effective and nominal interest rates. I’ve also included a link to an effective interest calculator, which can be helpful for learning and for making informed investment decisions.
Effective Annual Interest Rate: Definition, Formula, and Example by Investopedia - https://www.investopedia.com/terms/e/effectiveinterest.asp
Nominal and Effective Interest by Oxford University Press - https://global.oup.com/us/companion.websites/9780190296902/sr/interactive/formulas/nominal/
Effective Interest Rate Calculator - https://www.calculatorsoup.com/calculators/financial/effective-interest-rate-calculator.php